Applying the quantum approximate optimization algorithm to general constraint satisfaction problems

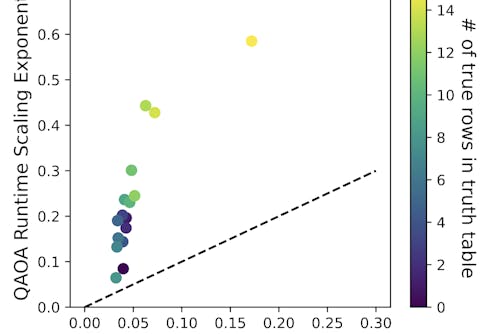
In this work we develop theoretical techniques for analysing the performance of the quantum approximate optimization algorithm (QAOA) when applied to random boolean constraint satisfaction problems (CSPs), and use these techniques to compare the complexity of a variety of CSPs, such as k-SAT, 1-in-k SAT, and NAE-SAT. Our techniques allow us to compute the success probability of QAOA with one layer and given parameters, when applied to randomly generated instances of CSPs with k binary variables per constraint, in time polynomial in n and k. We apply this algorithm to all boolean CSPs with k = 3 and a large number of CSPs with k = 4, k = 5, and compare the resulting complexity with the complexity of solving the corresponding CSP using the standard solver MapleSAT, determined experimentally. We find that random k-SAT seems to be the most promising of these CSPs for demonstrating a quantum-classical separation using QAOA.