Quantum speedups in solving near-symmetric optimization problems by low-depth QAOA

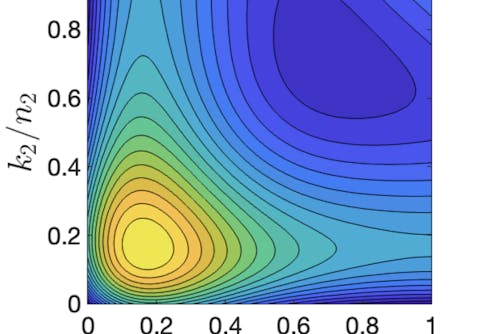
We present new advances in achieving exponential quantum speedups for solving optimization problems by low-depth quantum algorithms. Specifically, we focus on families of combinatorial optimization problems that exhibit symmetry and contain planted solutions. We rigorously prove that the 1-step Quantum Approximate Optimization Algorithm (QAOA) can achieve a success probability of Ω(1/ √ n), and sometimes Ω(1), for finding the exact solution in many cases. Furthermore, we construct near-symmetric optimization problems by randomly sampling the individual clauses of symmetric problems, and prove that the QAOA maintains a strong success probability in this setting even when the symmetry is broken. Finally, we construct various families of near-symmetric Max-SAT problems and benchmark state-of-the-art classical solvers, discovering instances where all known classical algorithms require exponential time. Therefore, our results indicate that low-depth QAOA could achieve an exponential quantum speedup for optimization problems.