Improving time dynamics simulation by sampling the error unitary
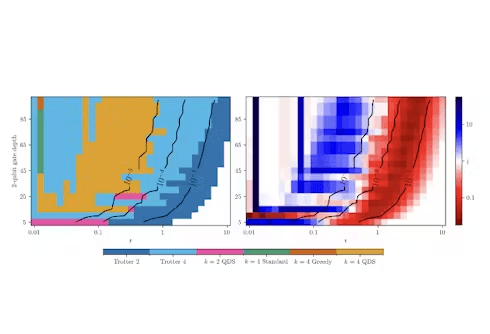
Performance comparison for Trotter 2, 4 and all variants of STEER for k = 2 and k = 4 in the 1 × 16 TF Ising model for different target times.
Content
We introduce an algorithm to improve the error scaling of product formulas by randomly sampling the generator of their exact error unitary. Our approach takes an arbitrary product formula of time t, with error O(t^(k+1)) and produces a stochastic formula with expected error scaling as O(t^(2(k+2))) with respect to the exact dynamics. For a given fixed error ϵ and total evolution time T this leads to an improved gate complexity. This is achieved by appending an additional circuit with depth at-most logarithmic in the number of qubits, and without needing extra ancillas. We prove that each instance of these stochastic formulas quickly concentrates to the expected value. These results are based on an exact characterization of the error unitaries for product formulas. Through extensive numerical simulations we assess the performance of this approach in several spin and fermionic systems. We show that the expansion of these error unitaries naturally leads to generalized Zassenhaus formulas, a result which could be of independent mathematical interest.
