Enhancing density functional theory using the variational quantum eigensolver

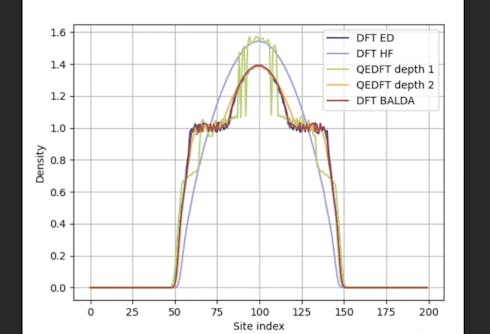
Quantum computers open up new avenues for modelling the physical properties of materials and molecules. Density Functional Theory (DFT) is the gold standard classical algorithm for predicting these properties, but relies on approximations of the unknown universal functional, limiting its general applicability for many fundamental and technologically relevant systems. In this work we develop a hybrid quantum/classical algorithm called quantum enhanced DFT (QEDFT) that systematically constructs quantum approximations of the universal functional using data obtained from a quantum computer. We benchmark the QEDFT algorithm on the Fermi-Hubbard model, both numerically and on data from experiments on real quantum hardware. We find that QEDFT surpasses the quality of groundstate results obtained from Hartree-Fock DFT, as well as from direct application of conventional quantum algorithms such as VQE. Furthermore, we demonstrate that QEDFT works even when only noisy, low-depth quantum computation is available, by benchmarking the algorithm on data obtained from Google’s quantum computer. We further show how QEDFT also captures quintessential properties of strongly correlated Mott physics for large Fermi-Hubbard systems using functionals generated on much smaller system sizes. Our results indicate that QEDFT can be applied to realistic materials and molecular systems, and has the potential to outperform the direct application of either DFT or VQE alone, without the requirement of large scale or fully fault-tolerant quantum computers.